In the Bitcoin ecosystem, your private key is essential for signing and authorising transactions, demonstrating your ownership of the funds. In contrast, the public key, as the name suggests, is the part of the key pair that can be safely shared with the public.
What is a public key?
A public key in Bitcoin is generated from the private key using a specific cryptographic algorithm.
This process is straightforward and computationally simple, involving elliptic curve multiplication, a one-way mathematical operation.
The crucial aspect of this key pair is that it’s easy to generate a public key from a private key, but practically impossible to do the reverse.
The complexity and nature of the mathematical operations involved make this one-way function secure.
This one-way function is fundamental to how cryptographic systems work.
It allows you to safely share your public key with others for verification purposes, such as confirming the authenticity of messages or transactions, without compromising the security of your private key.
The Role of Public Keys in Bitcoin
In the Bitcoin network, public keys are utilised primarily for the following purposes:
Creating a Bitcoin Address: The public key is essential in generating your Bitcoin address. This address, which you share with others to receive Bitcoin, is a hashed and encoded version of your public key. It’s designed to be shorter and more user-friendly, while maintaining a unique link to your original public key.
Verifying Transactions: Public keys play a crucial role in the verification of transactions. When you initiate a Bitcoin transaction, you sign it using your private key. This digital signature is then verified by others on the network using your corresponding public key. This process ensures that the transaction is legitimately authorised by the owner of the Bitcoins and remains unaltered.
Generating a Public Key
Fortunately, you’ll never have to manually perform this process yourself, as the software you use for Bitcoin transactions will handle it automatically. However, understanding how it works can provide valuable insight into Bitcoin’s security mechanics.
Firstly, your private key is a randomly generated 256-bit number, essentially a very large integer.
Bitcoin employs a specific type of cryptography known as Elliptic Curve Cryptography (ECC), utilising a particular elliptic curve designated as secp256k1.
On this curve, there exists a predefined and universally known point called the “generator point” (often denoted as ‘G’). This point is constant across the Bitcoin network.
The process involves multiplying your private key by this generator point. Note that this “multiplication” is a unique operation defined within the realm of elliptic curves, differing from traditional arithmetic multiplication.
The result of this multiplication is another point on the curve, characterised by both x and y coordinates. This resultant point is your public key. Put simply, the public key is calculated as: Public Key = Private Key * Generator Point.
Public keys are representable in two primary formats:
Compressed Format: This more space-efficient form starts with either ’02’ or ’03’, followed by the x-coordinate. The prefix (’02’ or ’03’) signifies the parity of the y-coordinate (even or odd, respectively).
Uncompressed Format: This includes both x and y coordinates and typically starts with ’04’.
Elliptic Curve Cryptography
Understanding Elliptic Curve Cryptography (ECC) is not necessary for everyday use of Bitcoin, such as buying, selling, or holding cryptocurrencies. However, a basic knowledge of how public and private keys are generated and function can be very helpful.
ECC is a form of public-key cryptography that relies on the algebraic structure of elliptic curves over finite fields. It plays a critical role in the security and functionality of Bitcoin.
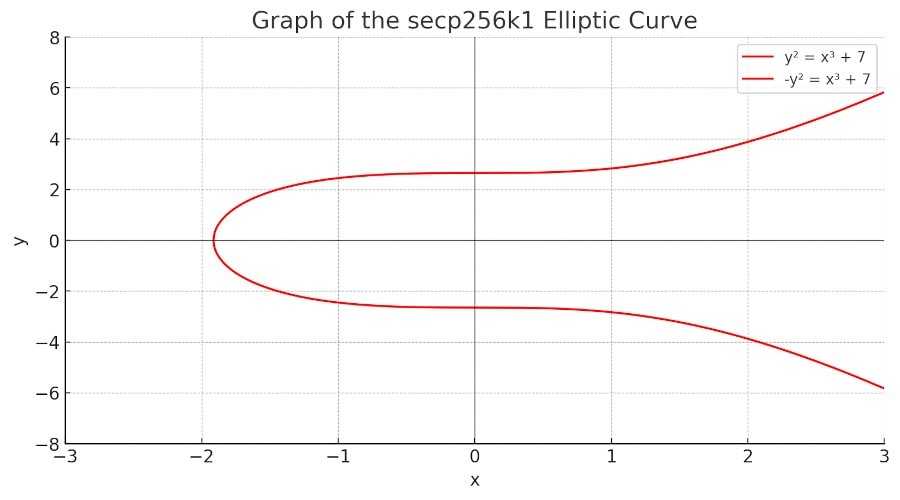
An elliptic curve is a mathematical concept, typically expressed by the equation y² = x³ + ax + b. These curves are chosen for their unique properties that make them ideal for cryptographic purposes, especially in creating hard-to-break security protocols.
The strength of ECC lies in the Elliptic Curve Discrete Logarithm Problem (ECDLP), a problem that is computationally challenging to solve, forming the basis of security in ECC systems. This complexity allows ECC to achieve high levels of security with smaller key sizes compared to traditional methods like RSA, resulting in faster computations and reduced resource requirements.
Bitcoin specifically utilises the `secp256k1` elliptic curve, defined by the simplified equation y² = x³ + 7. This means that the value of ‘a’ is 0, and ‘b’ is 7, a choice that significantly enhances computational efficiency. This efficiency is crucial, particularly in generating public keys from private keys, a foundational aspect of Bitcoin’s transaction process.
`secp256k1` is selected for its balance of security and performance. While it is secure enough for Bitcoin’s purposes, it’s important to note that different elliptic curves have varying security properties. The choice of this particular curve is also driven by its suitability for the decentralised and resource-conscious environment of Bitcoin.
In contrast to `secp256k1`’s prominence in Bitcoin, other domains, such as SSL/TLS for secure web communications, often use different elliptic curves like NIST P-256 or P-384. These curves are chosen based on the specific security needs and computational constraints of different applications.
The decision to use `secp256k1` in Bitcoin is a testament to the curve’s ability to facilitate efficient and secure cryptographic operations.
